Drawing Filled Quadrilaterals and Triangles
15th August 2022
This is an extension to my graphics libraries to plot filled quadrilaterals and triangles:

Coloured quadrilaterals drawn using the routine is this article,
on an Adafruit 240x240 colour TFT display.
It is designed for use with my colour TFT graphics library, Tiny TFT Graphics Library 2.
With one minor change it can also be used with the version of that library that supports reading from supported TFT displays, Reading from a TFT Display. It will probably also work with other graphics libraries.
The triangle and quadrilateral plotting routines share much of the same code, so the resulting routines are quite compact, and should fit on microcontrollers with limited memory.
You may wonder why I didn't just write a routine to plot filled triangles, and then draw quadrilaterals as two adjacent triangles. The answer is that with the libraries that support exclusive-OR plotting this results in a visible line between the two triangles, because that line is drawn twice; having a dedicated routine to plot quadrilaterals avoids this. In addition, this routine is faster.
Drawing filled quadrilaterals
Quadrilaterals are plotted by FillQuad(), which plots an arbitrary quadrilateral from the coordinates of its four vertices. For example, suppose the quadrilateral is the diamond shape shown below, defined by the coordinates x0,y0, x1,y1, x2,y2, and x3,y3. First the routine sorts the four coordinates in order of increasing y:
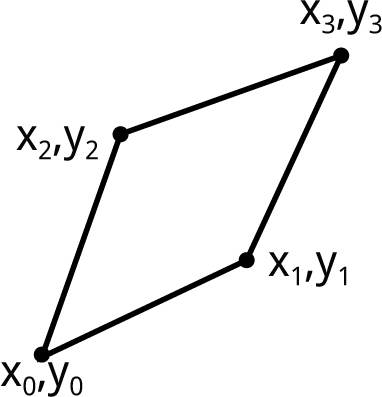
This takes five comparisons and up to five exchanges:
if (y0 > y1) { swap(y0, y1); swap(x0, x1); }
if (y2 > y3) { swap(y2, y3); swap(x2, x3); }
if (y1 > y3) { swap(y1, y3); swap(x1, x3); }
if (y0 > y2) { swap(y0, y2); swap(x0, x2); }
if (y1 > y2) { swap(y1, y2); swap(x1, x2); }
The routine swap() is defined as a macro, for efficiency.
Next, the quadrilateral is divided into three sections by drawing horizontal lines from x1,y1 to the opposite side at a point I'll call x4, and from x2,y2 to the opposite side at point x5:
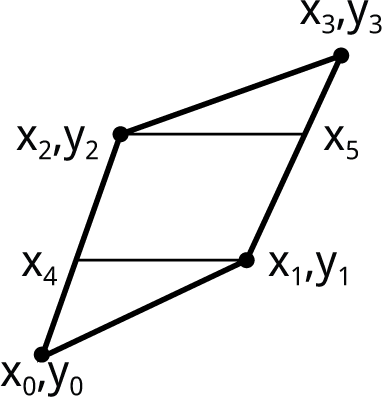
These x values are given by:
int16_t x4 = x0 + (x2 - x0) * (y1 - y0) / (y2 - y0); int16_t x5 = x1 + (x3 - x1) * (y2 - y1) / (y3 - y1);
Finally we fill each section by drawing a horizontal line for each integral value of y from y0 to y3. In each case the x coordinates of the line are calculated in a and b. The bottom section is filled with:
for (y = y0; y <= y1; y++) {
a = x0 + (x4 - x0) * (y - y0) / (y1 - y0);
b = x0 + (x1 - x0) * (y - y0) / (y1 - y0);
if (a > b) swap(a, b);
MoveTo(a, y); DrawTo(b, y);
}
The middle section is filled with:
for (; y <= y2; y++) {
a = x4 + (x2 - x4) * (y - y1) / (y2 - y1);
b = x1 + (x5 - x1) * (y - y1) / (y2 - y1);
if (a > b) swap(a, b);
MoveTo(a, y); DrawTo(b, y);
}
and the top section is filled with:
for (; y <= y3; y++) {
a = x2 + (x3 - x2) * (y - y2) / (y3 - y2);
b = x5 + (x3 - x5) * (y - y2) / (y3 - y2);
if (a > b) swap(a, b);
MoveTo(a, y); DrawTo(b, y);
}
Catering for special cases
There's one special case we need to treat differently, in a quadrilateral when x4 and x5 are both on the same side of the line from x0,y0 to x3,y3:
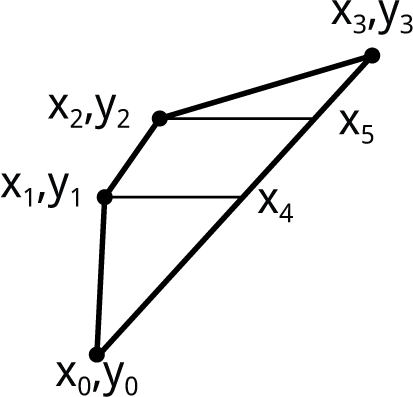
The routine tests for this situation, and converts it to the original configuration, with the code:
int16_t x4 = x0 + (x3 - x0) * (y1 - y0) / (y3 - y0);
int16_t x5 = x0 + (x3 - x0) * (y2 - y0) / (y3 - y0);
if ((x5 > x2) == (x4 > x1)) {
swap(x2, x5);
Concave quadrilaterals
FillQuad() doesn't currently handle concave quadrilaterals; for example:
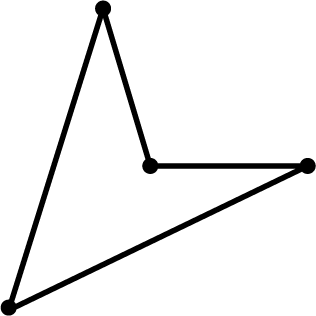
If necessary, draw these as two triangles.
Optimising the code
You may be tempted to try optimising the code by precalculating repeated subexpressions, and incrementing a and b in each of the three loops rather than recalculating them from scratch. However, I tried this and it made negligible difference to the execution time, probably because the compiler does a pretty good job of spotting such optimisations. I've therefore omitted them as they make the routine longer and harder to understand.
Drawing filled triangles
Triangles are drawn by FillTriangle(). this simple sorts the three coordinates in order of increasing y, and then calls the FillQuad() code with the last coordinate repeated twice.
Using the routines with different graphics libraries
The three occurrences of the line:
MoveTo(a, y); DrawTo(b, y);
should be the only thing you need to change if you're using these routines with a different graphics library.
If the library has a fast routine for drawing horizontal lines you'll get substantially better performance by using this. In my Tiny TFT Graphics Library 2 the most efficient way to draw a single pixel high horizontal line is to call FillRect(), as it bypasses the Bresenham line algorithm used by DrawTo(), so replace these three lines with:
MoveTo(a, y); FillRect(b - a + 1, 1);
This is over ten times faster, so I've made it the default choice; for example, plotting:
FillQuad(120, 120, 180, 150, 200, 200, 150, 180);
took 556ms using DrawTo(), and 41ms using FillRect() on a 20MHz ATtiny414.
Cubes demo
Here's a simple demo program to draw the stack of coloured cubes shown at the start of this article, consisting of 18 quadrilaterals:
void Cubes () {
int h = 21, w = 36, x0 = 120, y0 = 100;
for (int y=y0, i=2; y<=y0+h*6; y=y+h*3, i--) {
for (int x=x0-w*i; x<=x0+w*i; x = x+w*2) {
fore = Colour(255, 8, 8); // Red
FillQuad(x, y, x - w, y - h, x, y - h*2, x + w, y - h);
fore = Colour(16, 16, 255); // Blue
FillQuad(x - w, y - h, x, y - h*2, x, y - h*4, x - w, y - h*3);
fore = Colour(192, 128, 0); // Orange
FillQuad(x, y - h*2, x, y - h*4, x + w, y - h*3 ,x + w, y - h);
}
}
}
It's designed for a 240x240 or 320x240 display, but it should be easy to adapt it for other displays by changing the constants in the first line. I used the Adafruit 1.54" 240x240 colour TFT display, fitted to my TFT display backpack; see Universal TFT Display Backpack.
Resources
Here are the quadrilateral and triangle routines, and the demo program: Quadrilaterals and triangles.
Updates
17th August 2022: Forgot to include the macro swap(); added now.
blog comments powered by Disqus
