Silver Dollar Game: How to Win
10th January 2024
Last month I described the Silver Dollar Game, a logic game in which the aim is move five silver dollars, represented by illuminated LEDs, along a strip of 12 positions:

The Silver Dollar Game, in which you move five silver dollars represented by illuminated LEDs
along a row of 12 positions.
You take turns with the device to move one silver dollar to any blank position to its right, and the last player able to move wins the game. The game starts with a random position of five LEDs from which its possible to win, but unless you play perfectly the device will beat you.
This article explains the trick to winning against the device every time you play.
How to win
When it's your turn, calculate the Nim-sum of the position as follows:
Starting with the leftmost lit LED, count the number of unlit LEDs between alternate gaps. For example:
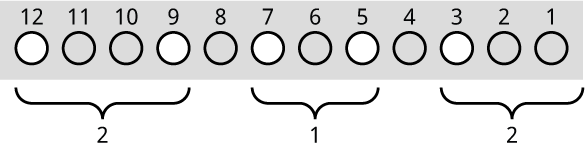
This is equivalent to a game of Nim with three heaps containing 2, 1, and 2 counters respectively.
The Nim-sum is the exclusive-OR of the sizes of the three heaps. In this case it is:
2 ^ 1 ^ 2 = 1
To win the game you need to make a move that converts the position to one with a Nim-sum of zero. In this case it's easy to see that a move that achieves this is:
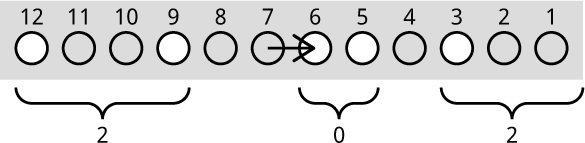
From now on, on your turn you will always be able to move to a position with a Nim-sum of zero until you've won the game.
A losing position
What about if, when it's your turn, the position already has a zero Nim-sum, as in this position?
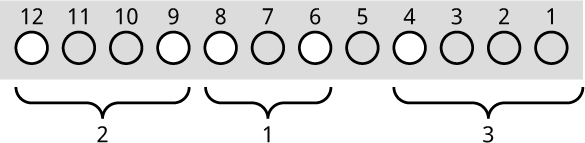
In this case the best you can do is make a random move and hope your opponent doesn't notice that they can make a winning move.
The program
The program uses the routine NimSum() to calculate the Nim-sum of a position:
uint8_t NimSum () {
uint8_t sum = 0;
for (int i=1; i<=Dollars; i=i+2) {
sum = sum ^ (Dollar[i-1] - Dollar[i] - 1);
}
return sum;
}
This calculates the exclusive-OR of the size of alternate gaps between the silver dollar positions in the array Dollar[], as described above.
The device's move is calculated by the routine FindBestMove():
int FindBestMove () {
int allmoves = 0, wins = 0, windollar = 0, winmove = 0, anydollar = 0, anymove = 0;
for (int i=1; i<=Dollars; i++) { // For each dollar
int moves = Dollar[i-1] - Dollar[i] - 1;
int start = Dollar[i-1];
for (int m=1; m<=moves; m++) {
Dollar[i-1] = start - m;
allmoves++;
if ((PseudoRandom() % allmoves) == 0) { anydollar = i; anymove = m; }
if (NimSum() == 0) {
wins++;
if ((PseudoRandom() % wins) == 0) { windollar = i; winmove = m; }
}
}
Dollar[i-1] = start;
}
if (wins > 0) return windollar<<8 | winmove;
else return anydollar<<8 | anymove;
}
If it finds a move that leaves the position with NimSum() equal to zero it chooses it. Otherwise it chooses any valid move.
If there are multiple possible winning or valid moves it uses a pseudo-random number generator, PseudoRandom(), to choose one at random, in order to make the play unpredictable.
blog comments powered by Disqus
