16 LEDs Solution and a New Puzzle
4th January 2022
Last month I gave the circuit and program for a puzzle consisting of 16 LEDs, 16 pushbuttons, and an ATtiny404 (or ATtiny204). Starting from a random position you had to find the correct sequence of button presses to turn all the LEDs on:

The 16 LEDs Puzzle, in which you have to press the buttons to light up all the LEDs.
This article explains how it works, and describes two alternative ways to solve it. Read the original article 16 LEDs Puzzle if you haven't yet built the circuit and want to try solving it yourself before reading the solution here.
I also give a program for a harder puzzle, called Kishi, that you can upload to the same board.
How it works
The puzzle was inspired by an online Flash game called Tacoyaki. When you press a button it toggles the state of the LED next to the button, and also the state of the LEDs on the same diagonals. For example, starting with all the LEDs off, if you press the button shown on the left, the LEDs will be illuminated in the pattern on the right:
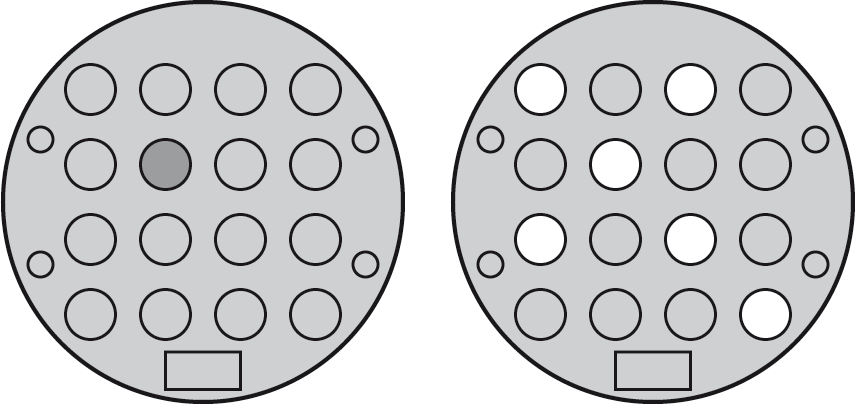
Pressing the same button twice undoes the effect of the first press, and the order of the button presses is irrelevant to the final pattern, so every pattern can be solved in at most 16 button presses. In fact there is some redundancy as you'll see in the general solution below.
In the Tacoyaki puzzle every button changes the state of either four or six LEDs. From this it's clear that every valid pattern has an even number of LEDs illuminated, so if you make the puzzle start from a totally random pattern of lights there's a chance that it will be impossible to solve.
How to solve it
One approach is to learn the solution for four common patterns. To solve the puzzle you can then use trial and error until you reach one of these patterns, and then apply the appropriate solution.
One row/column unlit
A common pattern is with one row or column of four LEDs unlit:
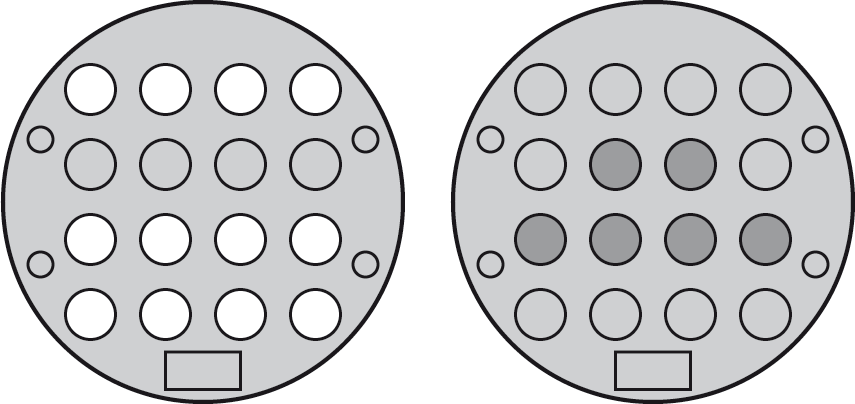
The right-hand diagram shows the buttons you need to press to solve this. If the row is in a different position, or vertical, you can just translate the solution in the same way.
Two rows/columns unlit
A pattern with two rows/columns unlit, as on the left below, is also easy to solve:
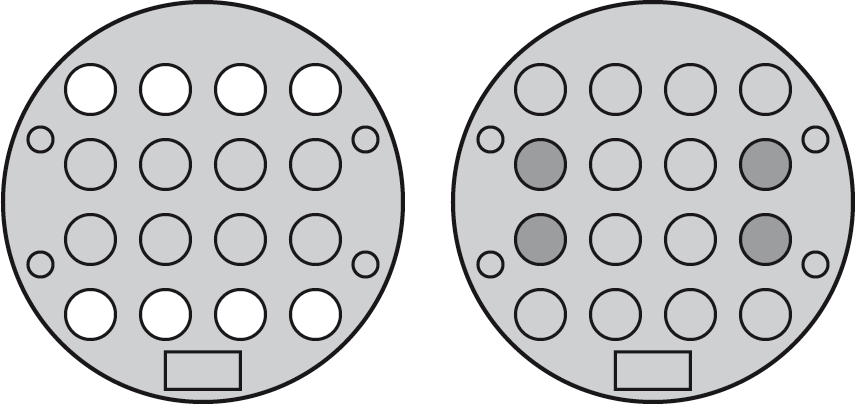
Just press the four buttons shown on the right.
Two LEDs unlit
Another common pattern is with just two LEDs unlit in the arrangement shown on the left:
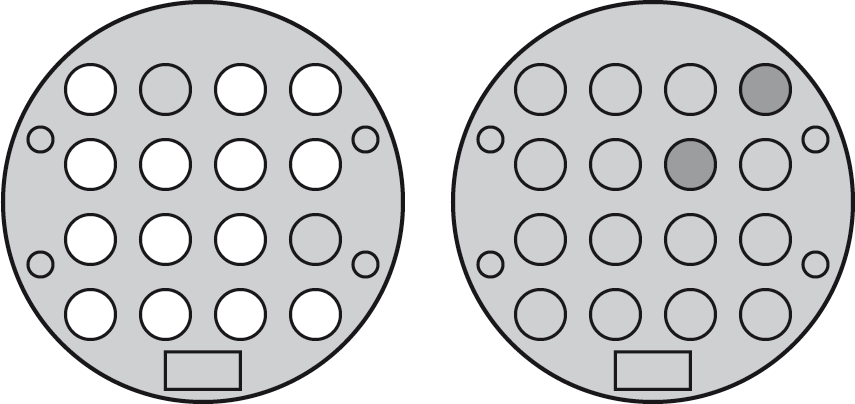
The solution is to press the two buttons shown on the right. Again you can transform the solution to cater for rotations and mirror images.
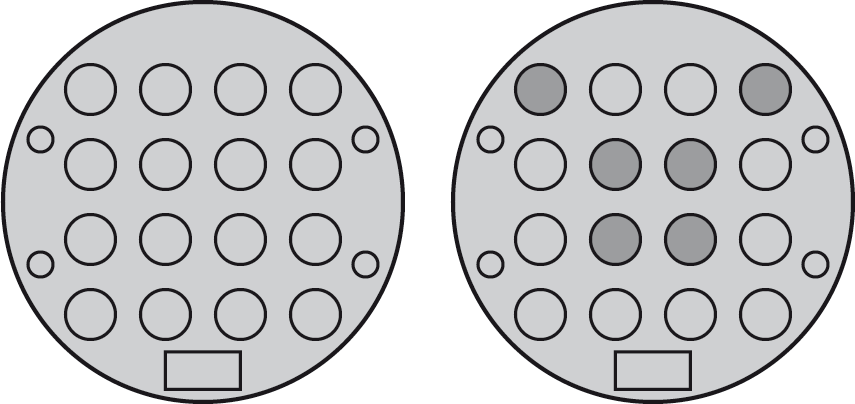
All LEDs off
Finally, if you get the puzzle to the state with all LEDs off, as shown on the left, you can turn them all on by pressing the six buttons shown on the right:
A general solution
If you prefer you can use the following method to solve any position. First consider the LEDs and buttons numbered as follows:
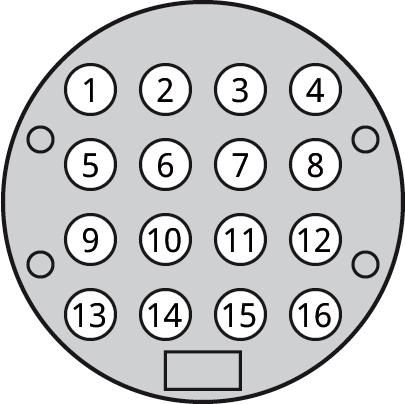
Note down the pattern of LEDs in the starting position that you want to solve. Then press buttons as instructed using the following table:
| Press this button | If these LEDs were lit |
| 1 | None or two of 1, 9, and 14 |
| 2 | One of 4 and 7 |
| 4 | None or two of 4, 7, and 10 |
| 5 | One of 4 and 10 |
| 6 | None or two of 6, 9, and 11 |
| 7 | None or two of 2, 7, and 10 |
| 9 | One of 1 and 6 |
| 10 | None or two of 5, 7, and 10 |
| 11 | None or two of 6, 11, and 14 |
| 14 | One of 1 and 11 |
Every pattern can be solved in at most 10 button presses, and you never need to press buttons 3, 8, 12, 13, 15, or 16.
Note that the question in the right-hand column always applies to the puzzle's original state, not the current state after a few button presses.
The way this table was derived depends on some mathematics using matrix operations called Gaussian elimination, and is beyond the scope of this article [1].
Kishi puzzle
Finally here's a program that works with the same circuit to provide a new puzzle I've called Kishi, the Japanese for knight, after the knight's move it's based on. It's quite a bit harder than the original puzzle.
In this puzzle pressing a button toggles the state of the LED next to it, and also the state of the LEDs a knight's move away. For example, starting with all the LEDs off, if you press the button shown on the left in the following diagrams, the LEDs will be illuminated in the pattern of the right:
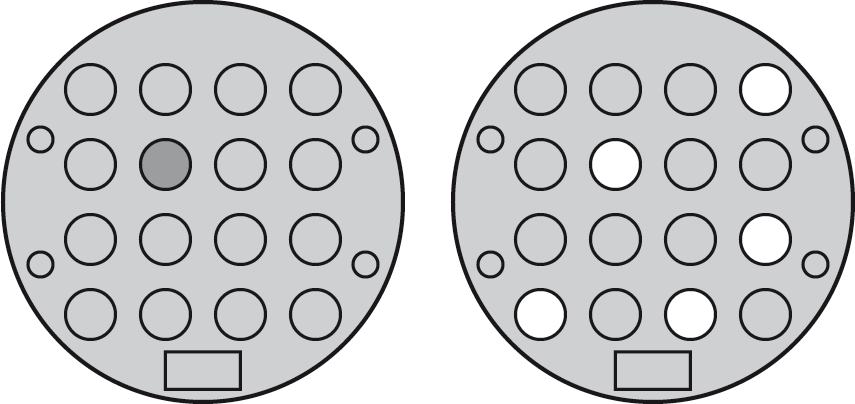
Unlike the Tacoyaki puzzle, in Kishi every pattern of LEDs can be solved, and every pattern has a unique solution.
Here to whet your appetite is a starting pattern of LEDs on the left, and the pattern of buttons you have to press to solve it on the right:
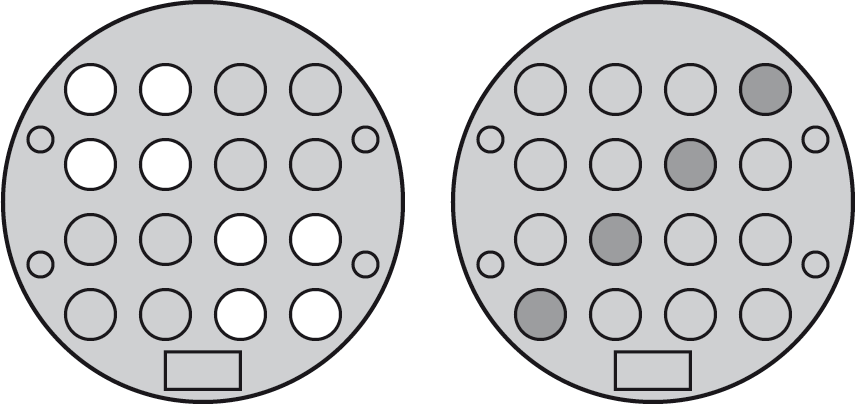
Here's the program for the Kishi puzzle: 16 LEDs Kishi Puzzle Program.
Follow the instructions in the previous article 16 LEDs Puzzle to upload it.
If you're stuck, here's the solution: 16 LEDs Kishi Puzzle Solution.
- ^ Thanks to John Tromp for the analysis; see Flip puzzles and linear algebra.
blog comments powered by Disqus
